Index
Definitions
- Information security: protecting information and information systems from unauthorized access, use, disclosure, disruption, modification, or destruction.
Security Properties
- Confidentiality:
- No improper disclosure of information. or
- No unauthorized access to information.
-
Privacy: Confidentiality of information that you don’t want to share.
-
Anonymity: Confidentiality of your identity.
- Integrity:
- No improper modification of information. or
- No unauthorized modification of information.
- Availability:
- No improper impairment of functionality/service. or
- No unauthorized impairment of functionality
-
Authentication: Principals or data origin can be identified accurately
-
Non-repudiation: Actions done cannot be denied
- Accountability: Actions can be traced to responsible principals
Encryption Scheme

where $E(Key_1, P) = C$ and $D(Key_2, C) = P$.
- Symmetric algorithms:
- $Key_1 = Key_2$, or are easily derived from each other.
- Asymmetric algorithms:
- $Key_1 \neq Key_2$
- Public key can be published without compromising private key.
Security depends only on secrecy of the key, not on the algorithm
Mathematical Formalization
Let $M$ be the message space, and $m \in M$ is plaintext.
Similarly, let $C$ be the ciphertext space, and $c \in C$ is ciphertext.
Let $K$ be the key space, and $e, d \in K$.
For each $e \in K$ determines a bijective function $E_e$ from $M$ to $C$, and similarly, for each $d \in K$ determines a bijective function $D_d$ from $C$ to $M$.
So we could represent as follows:
$E_e(M) = C$ or $E(M, e) = C$
and
$D_d(C) = M$ or $D(C, d) = M$
Since that the encryption function $E$ and decryption function $D$ are bijiective, for each element in set $M$ and $C$ should have its pair in the opposite set.
Characteristics of Cryptographic Systems
- Type of operations used to transform plaintext into ciphertext
- based on two general principles:
- Substitution: each element in plaintext (bit, letter) is mapped into another element.
- Transposition: elements in plaintext are rearranged
- Most systems involve multiple stage substitutions and transpositions.
- based on two general principles:
- Number of keys used
- Symmetric, single-key, secret-key, or conventional encryption: sender and receiver use same key
- Asymmetric, two-key, public-key encryption: sender and receiver use different keys
- Way in which plaintext is processed
- Block cipher: processes input one block of elements at a time, producing an output block for each input block.
- Stream cipher: processes input elements continuously, producing in output one element at a time, as it goes along.
Symmetric key encryption
For symmetric encryption scheme $\{E_e | e \in K\}$ and $\{D_d | d \in K\}$, $\{e, d\}$ are easy to derived from each other or just $e = d$
- Also known as: secret-key, single-key, one-key, shared-key, conventional encryption.
Historical Ciphers
Caesar Cipher
$C = E(K, M) = (M + K) \mod 26$
$M = D(K, C) = (C - K) \mod 26$
where $M, C \in Alphabets$ and $Alphabets$ are mapped into $\{0, 1, …, 25\}$
Especially, when we set $K = 13$, the function is called ROT13, where $E$ is equivalent to $D$
Mono-alphabetic substitution ciphers
Map a element in $A$ into a element in $C$
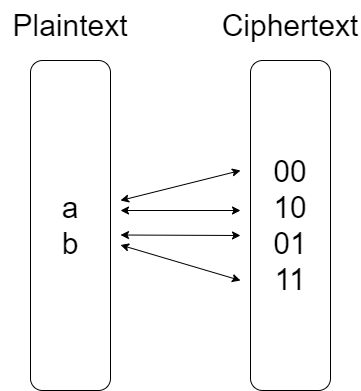
Homophonic substitution ciphers
Map a element in $A$ into multiple elements in $C$
For communicators: This relationship/set is the key
For cryptanalysis: frequency analysis is more difficult
For example:
for $A = \{x, y\}$, declares keys $K_x = \{00, 10\}$ and $K_y = \{01, 11\}$.
The plaintext xy encrypts to one of 0001, 0011, 1001, 1011
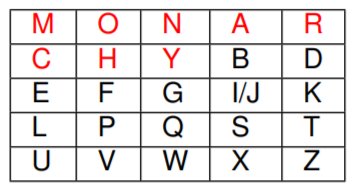
Playfair Cipher
steps:
- Pick keyword (here: monarchy)
- Construct matrix: fill in letters of keyword (minus duplicates) left2right & top2bottom, and remaining letters in alphabetic order, where I and J count as one letter.
- Plaintext is encrypted two letters at a time:
- If a pair is a repeated letter, insert filler like ‘X’ (e.g., “BALLOON” ; “BA LX LO ON”). Add an ‘X’ also at the end, if needed (or any other character).
- If both letters fall in the same row, replace each with letter to right, wrapping back to start from end (e.g., “AR” is encrypted as “RM”).
- If both letters fall in the same column, replace each with the letter below it, wrapping to top from bottom (e.g., “MU” is encrypted as “CM”).
- Otherwise each letter is replaced by the letter in the same row and in the column of the other letter of the pair (e.g., “HS” becomes “BP” and “EA” becomes “IM”, or “JM”, as the encipherer wishes)
Vigenere Cipher (polyalphabetic substitution cipher)
- a sequence of plaintext letters $P = p_0, p_1, p_2, …, p_{n−1}$,
- a key consisting of the sequence of letters $K = k_0, k_1, k_2, …, k_{m−1}$, typically $m < n$.
The encryption/decryption is as follows:
$C_i = (P_i + k_{i \mod m}) \mod 26$
and
$P_i = (C_i − k_{i \mod m}) \mod 26$

Vernam Cipher
$P \oplus K = C$
$C \oplus K = P$
Rail Fence Cipher

Columnar transposition cipher
Example:

Also, we could perform another encryption to be more secure.
Feistel Cipher
Composite (product) ciphers: combining both substitution and transposition
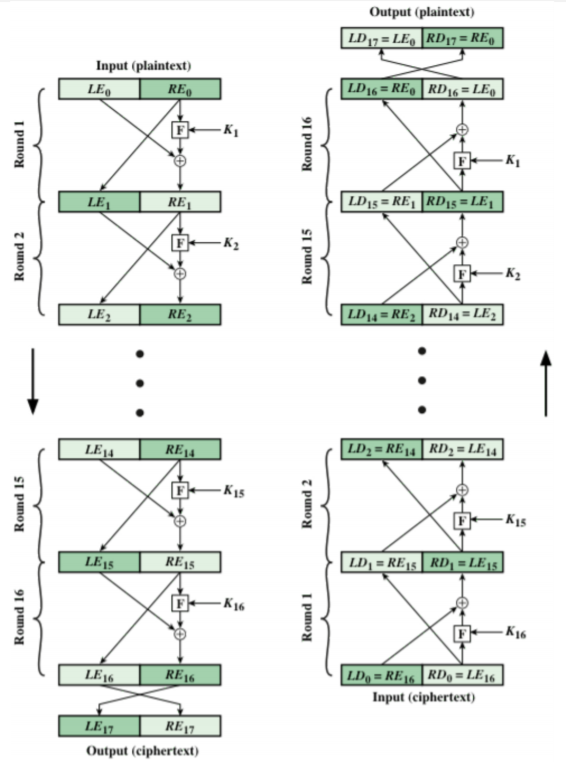
Encryption:
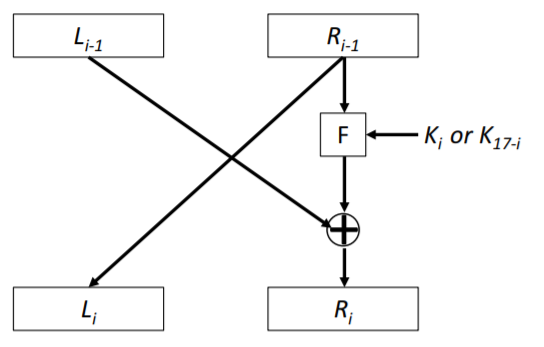
$LE_i = RE_{i - 1}$
$RE_i = LE_{i - 1} \oplus F(RE_{i - 1}, K_i)$
Decryption:
Since $LD_{16 - i} = RE_i$ and $RD_{16 - i} = LE_i$
$LD_i = RD_{i - 1}$
$RD_i = LD_{i - 1} \oplus F(RD_{i - 1}, K_{17 - i})$
Proof:
$\begin{equation}
\begin{split}
LD_i
& = RE_{16 - i} \\
& = LE_{16 - i - 1} \oplus F(RE_{16 - i - 1}, K_{16 - i}) \\
& = LE_{15 - i} \oplus F(RE_{15 - i}, K_{16 - i}) \\
& = RD_{16 - 15 + i} \oplus F(LD_{16 - 15 + i}, K_{16 - i}) \\
& = RD_{i + 1} \oplus F(LD_{i + 1}, K_{16 - i}) \\
& = RD_{i + 1} \oplus F(RD_i, K_{16 - i})
\end{split}
\end{equation}$
$\begin{equation}
\begin{split}
RD_i
& = LE_{16 - i} \\
& = RE_{16 - i - 1} \\
& = RE_{15 - i} \\
& = LD_{16 - 15 + i} \\
& = LD_{i + 1}
\end{split}
\end{equation}$
DES Encryption
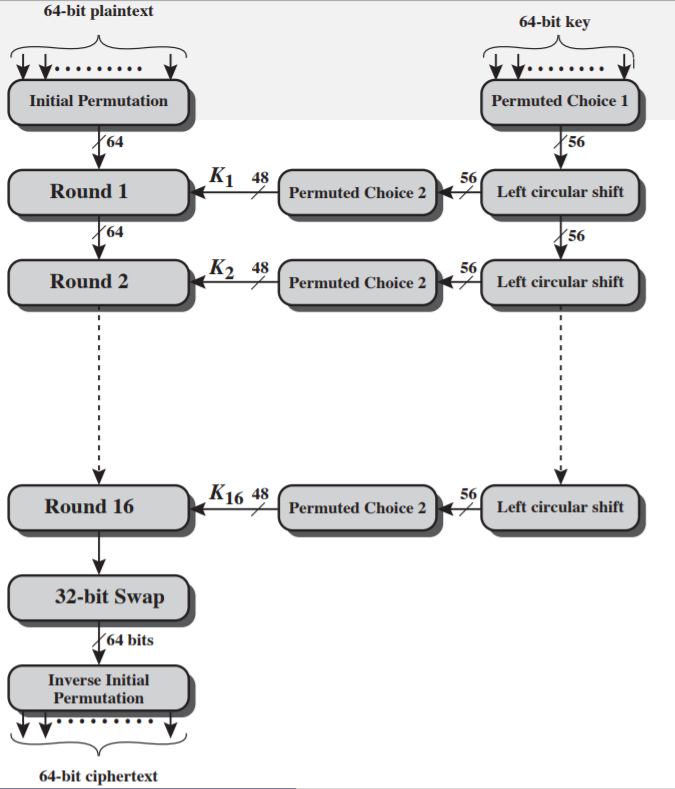
-
Block size: 64 bits
-
Key size: 56 bits (last 1 bit for each 7 bits used to validate the key itself)
-
Key validation:
$\sum\limits_{i=1}^8 b_{8k + i} \equiv 1 \mod 2, 0 \leq k \leq 7$
- Single Round:
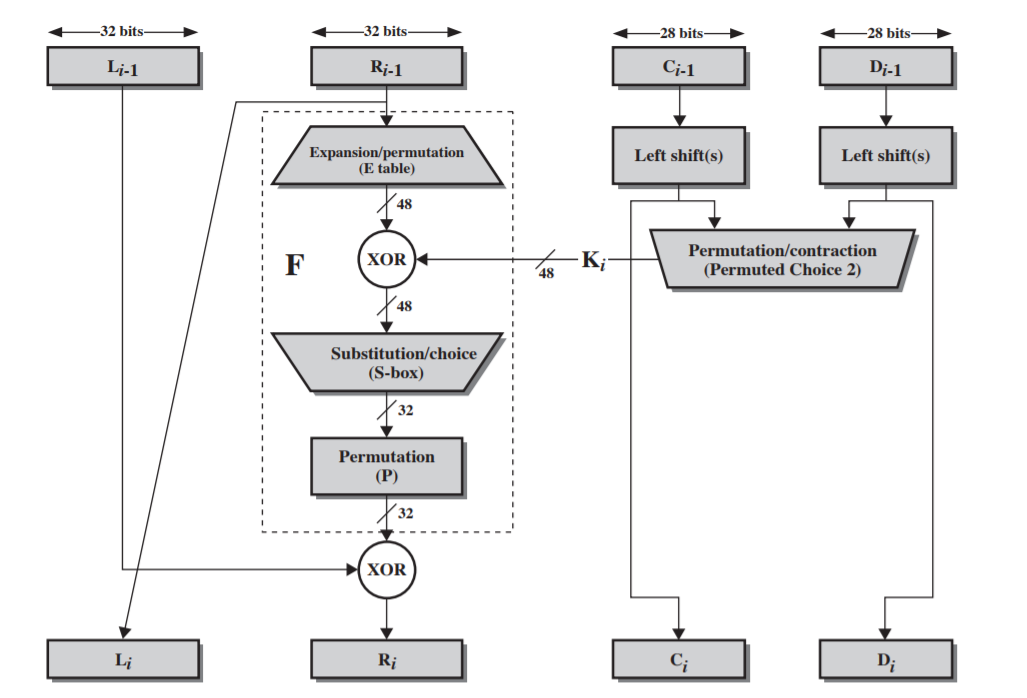
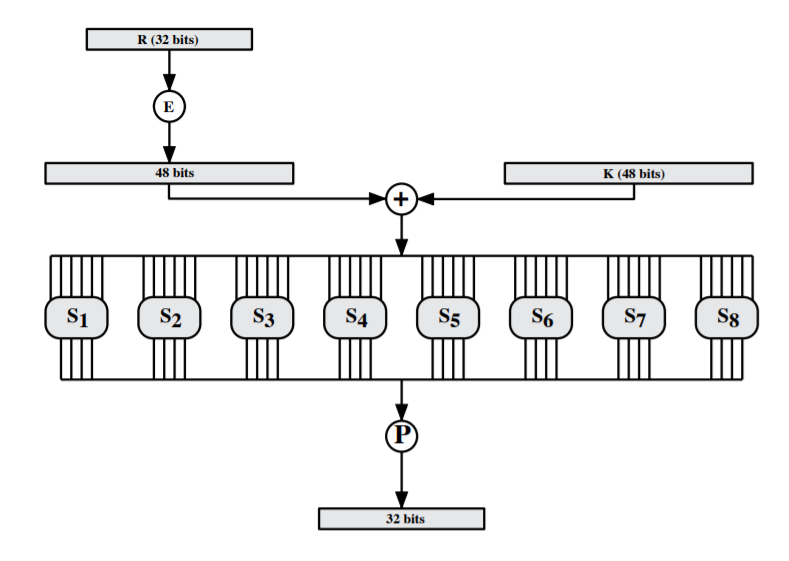
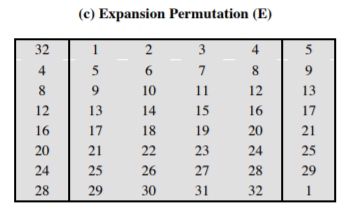
- Expansion:
- Substitution:
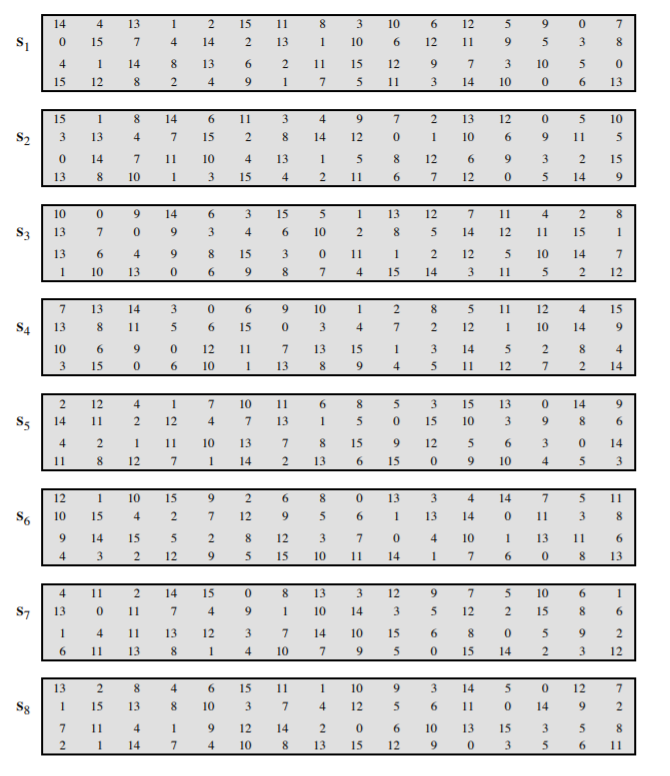
- Permutation:
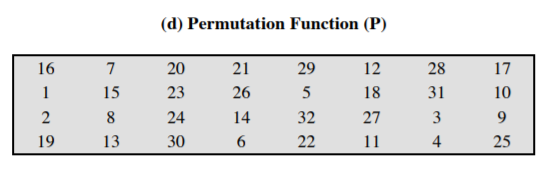
- Expansion:
- Key generation:
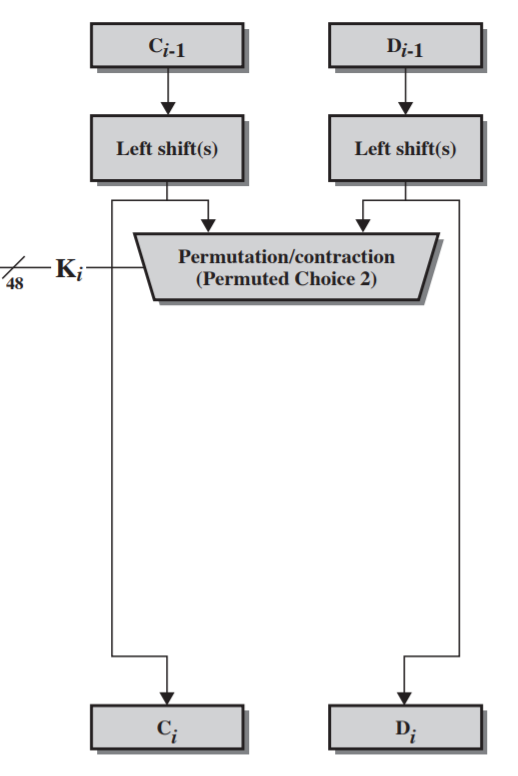
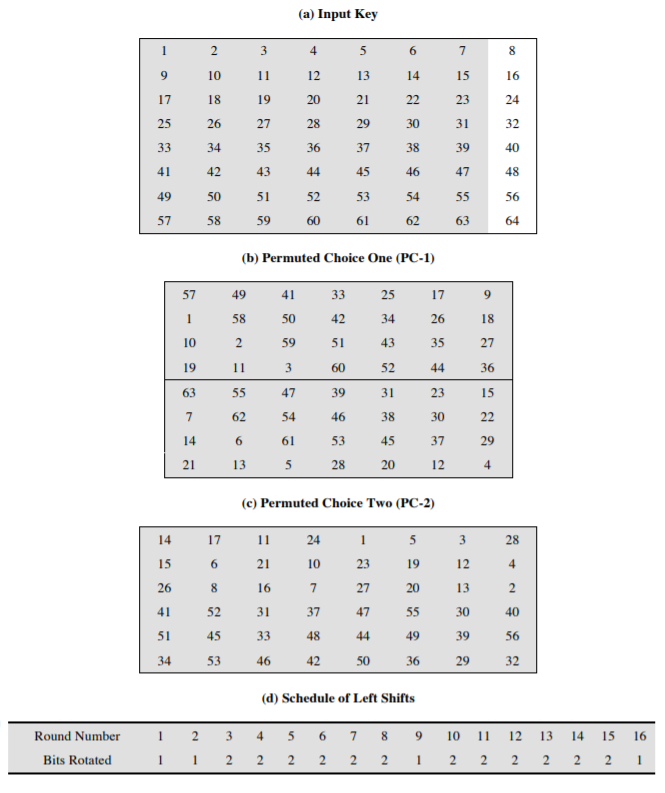
DES Security
-
two DES encryptions:
Meet in the middle attack:
Find two keys satisfying $E(K_1, P) = D(K_2, C)$
-
Triple DES
$C = E(K_1, D(K_2, E(K_1, P)))$ or $C = E(K_1, E(K_2, E(K_3, P)))$
For two keys in T-DES:
- Compatibility is maintained with standard DES $(K_2 = K_1)$.
- No known practical attack
S-DES
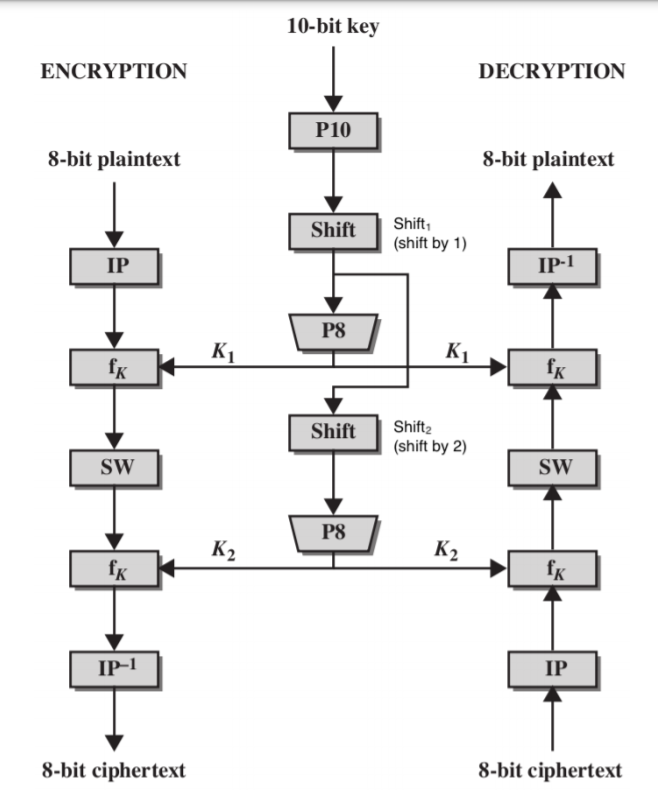
-
IP

-
$f_k$
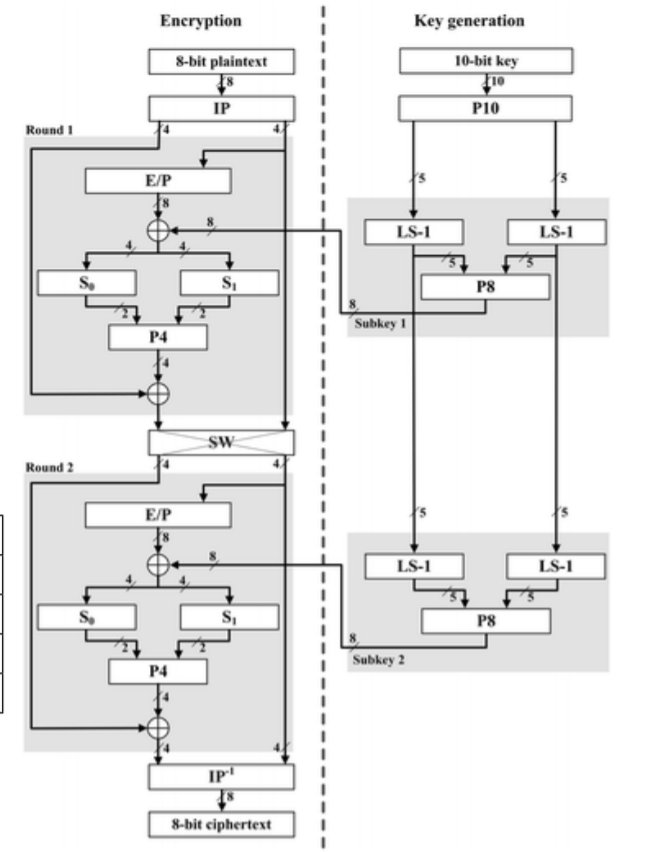
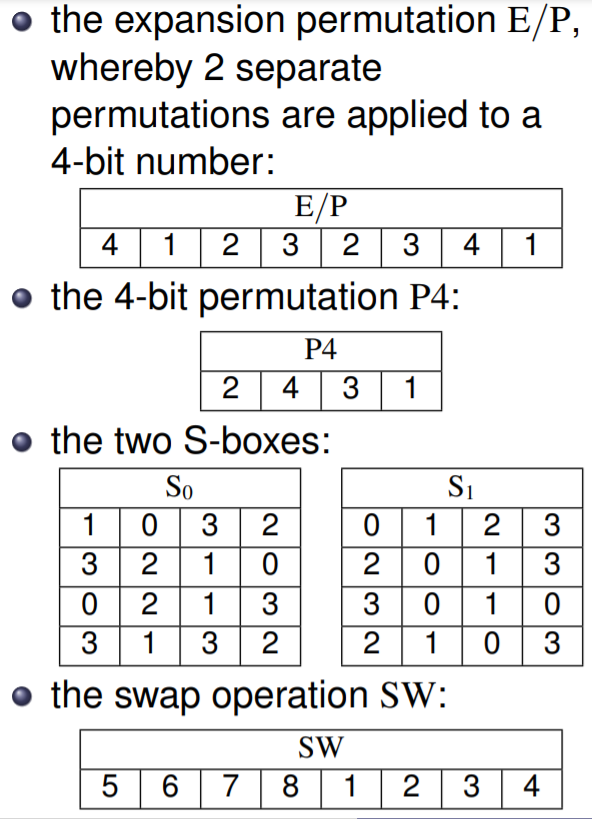
-
Key generation:

Block Cipher Modes
ECB
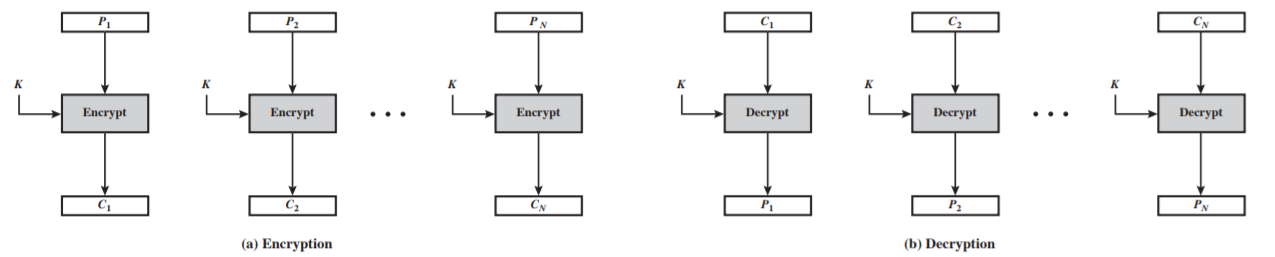
-
Encryption: $C_i = E(P_i, K)$
-
Decryption: $P_i = E(C_i, K)$
-
Properties:
- Same encrypted block if the plaintext is same
- Could parallel process
CBC
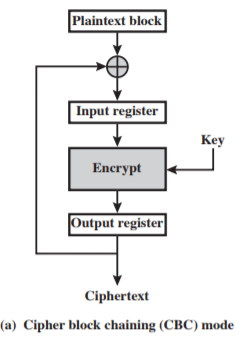

-
Encryption:
$C_1 = E(K, IV \oplus P_1)$
$C_i = E(K, C_{i - 1} \oplus P_i)$, $i \geq 1$ -
Decryption:
$P_1 = D(K, C_1) \oplus IV$
$P_i = D(K, C_i) \oplus C_{i - 1}$, $i \geq 1$ -
Properties:
- need pad last block if not full
- if an error occurs (changed bits, dropped blocks) in Ci but not Ci+1, then Ci+2 is correctly decrypted.
CFB

-
Encryption:

$C_i = P_i \oplus MSB_s(E(K, reg))$
$MSB_s(X)$ is the most significant $s$ bits of $X$,
$reg$ is the register initially contains IV, and fill with the $C_i$ afterwards.
Every encryption shifts the $reg$ $s$ bits to refresh value.
-
Decryption:
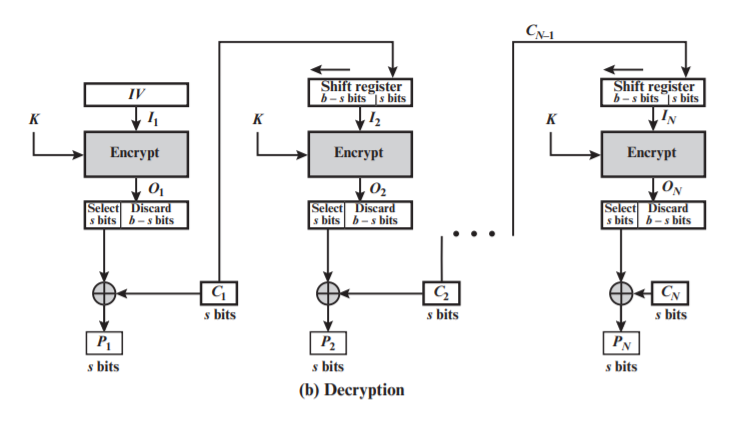
$P_i = C_i \oplus MSB_s(E(K, reg))$
-
Properties:
- Only use encryption function
- Act like stream cipher
OFB

-
Encryption/Decryption:

$C_i = P_i \oplus E(MSB_s(K, reg))$
$P_i = C_i \oplus E(MSB_s(K, reg))$
-
Properties:
- Similar as CFB, except that OFB uses encrypted block to xor with text
Number Theory
-
GCD & Extended GCD
- GCD
gcd(a, b): if b == 0 then return a else return gcd(b, a mod b) - Extended GCD
exgcd(a, b): if b == 0 then return (a, 1, 0) else (d', x', y') <- exgcd(b, a mod b) return (d', y', x' - (int(a / b) * y))
- GCD
RSA
-
Primitives
We must get two factors $p$ and $q$ of $n$, which is hard.
- Generate keys
-
Select prime numbers
$p, q$
- Calculate $n = p * q$ and $\phi(n) = (p - 1) * (q - 1)$
-
select $e$ where,
$1 < e < \phi(n)$, relatively prime to $\phi(n)$
- Compute $d = e^{-1} \mod \phi(n)$
- Set public key $(e, n)$ and private key $(d, n)$
-
-
Encryption and Decryption
$C = M^e \mod n$
and
$M = C^d \mod n$
Asymmetric algorithms for distribution
-
Digital envelope
Using asymmetric algorithm to encrypt symmetric key, for example, RSA
Sender: $C = (C_1, C_2) = (K^e \mod n, E(M, K))$
Receiver: $K = C_1^d \mod n$ and then $M = D(C_2, K)$
-
Key exchange algorithms
Diffie-Hellman Key Exchange
-
Discrete logarithms
$\forall b \in \mathbb{Z}, \exists i \in \{1,…,p-1\}$, there is $b = s^i \mod p$
In other words: for any integer b and a primitive root s of prime number p, we can find a unique exponent i such that
$b = s^i \mod p$ where $1 \leq i \leq (p − 1)$.
- Key exchange
- share a prime number $q$ and an integer $\alpha$ which is a primitive root of $q$
- A and B generate random numbers, $X_A$ and $X_B$ for A and B, respectively
- A and B computes $Y_i = \alpha^{X_i} \mod q$, where $i \in \{A, B\}$
- exchange $Y_A$ and $Y_B$
- compute $K = Y_A^{X_B} \mod q = Y_B^{X_A} \mod q$
- Group DH exchange

- El Gamal
- $A \rightarrow B$: $Y_A = \alpha^{X_A} \mod q$
- $B \rightarrow A$: $(C, Y_B)$ = $(E(M, K), \alpha^{X_B} \mod q)$
- $A$: $K = Y_B^{X_A} \mod q$, $M = D(C, K)$
Hash
- Hash function:
- Maps an input with arbitrary bit length to an output of fixed bit length
- computable in limited time
- Cryptographic hash function:
- One-way, it is hard to get $x$ when only given $y = h(x)$
- It’s difficult to find $x’$ that $h(x) = h(x’)$
- MAC (Message Authentication Code):
- Family of hash functions parameterized by secret key
- given $(x_i, h_K(x_i))$, it is infeasible to compute $(x, h_K(x))$ for $x \neq x_i$
Security Protocols
Needham-Schroeder Public Key Protocol (NSPK)
Procedure
- $A \rightarrow B: \{NA, A\}_{K_B}$
- $B \rightarrow A: \{NA, NB\}_{K_A}$
- $A \rightarrow B: \{NB\}_{K_B}$
MITM
- $A \rightarrow C: \{NA, A\}_{K_C}, C \rightarrow B: \{NA, A\}_{K_B}$
- $B \rightarrow C: \{NA, NB\}_{K_A}, C \rightarrow A: \{NA, NB\}_{K_A}$
- $A \rightarrow C: \{NB\}_{K_C}, C \rightarrow B: \{NB\}_{K_B}$
NSL Protocol
Procedure
- $A \rightarrow B: \{NA, A\}_{K_B}$
- $B \rightarrow A: \{NA, NB, B\}_{K_A}$
- $A \rightarrow B: \{NB\}_{K_B}$
MITM
- $A \rightarrow C: \{NA, A\}_{K_C}, C \rightarrow B: \{NA, A\}_{K_B}$
- $B \rightarrow C: \{NA, NB, B\}_{K_A}$, $C \rightarrow A: \{NA, NB, B\}_{K_A}$
$A$ received the message $\{NA, NB, B\}$ and found that $A$ is connecting to $B$ (should be $C$).
Zero-knowledge Protocols
Principals
- Prover: $Peggy$
- Verifier: $Victor$
- Trusted Third Party: $Trent$
Setup
- $Trent$: choose prime numbers $p$, $q$, publish $n = p * q$
- $Peggy$: choose $s$ where $1 < s < n - 1$, and publish $v = s^2 \mod n$
- $Victor$: knows $v$ and $n$
Verification (Peggy knows s)
- $Peggy$: choose $r$ where $1 < r < n - 1$, calculate $x = r^2 \mod n$ and send to $Victor$
- $Victor$: send challenge $c$ where $c \in \{0, 1\}$
- $Peggy$: calculate $y = (r * s^c) \mod n$
- $Victor$: calculate $A = y^2 \mod n$ and $B = (x * v^c) \mod n$ and check if $A = B$
Proof:
$\begin{equation}
\begin{split}
y^2 \mod n
& = (r * s^c)^2 \mod n \\
& = (r^2 * s^2c) \mod n \\
& = (r^2 * (S^2)^c) \mod n \\
& = (x * v^c) \mod n
\end{split}
\end{equation}$
Cheating
Principal
- $Pamela$: Only knows $v = s^2 \mod n$
Cheat
- $Victor$ choose $c = 0$
- $Pamela$: choose $r$ where $1 < r < n - 1$, set $x = r^2 \mod n$
- $Victor$: choose $c = 0$
- $Pamela$: set $y = r \mod n$
- $Victor$: check $y^2 \mod n$ and $(x * v^0) \mod n$
- $Victor$ choose $c = 1$
- $Pamela$: choose $r$ where $1 < r < n - 1$, set $x = \frac{r^2}{v} \mod n$
- $Victor$: choose $c = 1$
- $Pamela$: set $y = r \mod n$
- $Victor$: check $y^2 \mod n$ and $(x * v^1) \mod n$